Question

In each of the following


`find \: (dy)/(dx)\:`

`a)\: \: y = \sin ^ - 1 √(x) + ln( √(x) )`


`b) {e}^(y) = {2}^(x) log(x) - {e}^(2x)`
​

Answer 1

(a) Recall that

`(\mathrm d[\sin^(-1)x])/(\mathrm dx)=\frac1{√(1-x^2)}`

`(\mathrm d[\ln x])/(\mathrm dx)=\frac1x`

`(\mathrm d[\sqrt x])/(\mathrm dx)=\frac1{2\sqrt x}`

Then by the chain rule,

`y=\sin^(-1)(\sqrt x)+\ln(\sqrt x)`

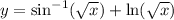
`\implies(\mathrm dy)/(\mathrm dx)=(\mathrm d[\sin^(-1)(\sqrt x)+\ln(\sqrt x)])/(\mathrm dx)`

`=\frac1{√(1-(\sqrt x)^2)}(\mathrm d[\sqrt x])/(\mathrm dx)+\frac1{\sqrt x}(\mathrm d[\sqrt x])/(\mathrm dx)`

`=\frac1{2\sqrt x√(1-x)}+\frac1{2(\sqrt x)^2}`

`=\frac1{2√(x-x^2)}+\frac1{2x}`

`=\boxed{(x+√(x-x^2))/(2x√(x-x^2))}`

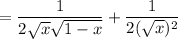
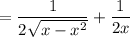
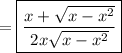
(b) I'll assume
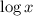`\log x` refers to the logarithm of base
`e`. Recall that

`(\mathrm d[e^x])/(\mathrm dx)=e^x`

`2^x=e^(\log2\,x)\implies(\mathrm d[2^x])/(\mathrm dx)=e^(\log2\,x)(\mathrm d[\log2\,x])/(\mathrm dx)=\log2\cdot2^x`

Then using the chain rule and implicit differentiation, we get

`e^y=2^x\log x-e^(2x)`

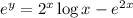
`\implies e^y(\mathrm dy)/(\mathrm dx)=(\mathrm d[2^x])/(\mathrm dx)\log x+2^x(\mathrm d[\log x])/(\mathrm dx)-e^(2x)(\mathrm d[2x])/(\mathrm dx)`

`e^y(\mathrm dy)/(\mathrm dx)=\log2\cdot2^x\log x+\frac{2^x}x-2e^(2x)`

`(\mathrm dy)/(\mathrm dx)=\frac{\log2\cdot2^x\log x+\frac{2^x}x-2e^(2x)}{e^y}`

`(\mathrm dy)/(\mathrm dx)=\frac{\log2\cdot2^x\log x+\frac{2^x}x-2e^(2x)}{2^x\log x-e^(2x)}`

`(\mathrm dy)/(\mathrm dx)=\boxed{(\log2\cdot2^xx\log x+2^x-2xe^(2x))/(x(2^x\log x-e^(2x)))}`

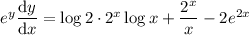
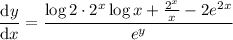
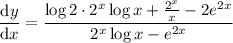
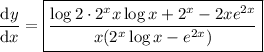
If instead
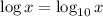`\log x=\log_(10)x` denotes the base 10 logarithm, you need only make the following adjustment:

`\log x=(\ln x)/(\ln 10)\implies(\mathrm d[\log_(10)x])/(\mathrm dx)=\frac1{\ln10\,x}`

where
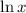`\ln x` is logarithm of base
`e`.