Question

Eric is studying people's typing habits. He surveyed 525 people and asked whether they leave one space or two spaces after a period when typing. 440 people responded that they leave one space. Create a 90% confidence interval for the proportion of people who leave one space after a period. Round your results to four decimal places.

Answer 1

Answer: (0.8115, 0.8645)

Explanation:

Let p be the proportion of people who leave one space after a period.

Given: Sample size : n= 525

Number of people responded that they leave one space. =440

i.e. sample proportion:
`\hat{p}=(440)/(525)\approx0.838`

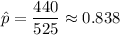
z-score for 90% confidence level : 1.645

Formula to find the confidence interval :

`\hat{p}\pm z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`

`0.838\pm (1.645)\sqrt{(0.838(1-0.838))/(525)}\\\\=0.838\pm (1.645)√(0.00025858285)\\\\=0.838\pm (1.645)(0.01608)\\\\= 0.838\pm0.0265\\\\=(0.838-0.0265,\ 0.838+0.0265)\\\\=(0.8115,\ 0.8645)`

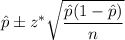
Hence, a 90% confidence interval for the proportion of people who leave one space after a period: (0.8115, 0.8645)