Question

An economist wishes to conduct a survey in two different cities in the same county to determine the difference in the proportions of residents who believe that economy is improving under president Trump. A 99% confidence interval is to be constructed for the difference between the proportions. If the sample sizes for both cities are to be equal, find the minimum sample size needed for each city so that the margin of error not to exceed 6%.

Answer 1

The minimum sample size needed for each city = 922

Explanation:

From the information given:

the objective is to find the minimum sample size needed for each city so that the margin of error not to exceed 6%.

If we take a look at the question very well:

we are only given the confidence interval of 99% and the margin of error of 6%

we were not informed or given the value or estimate of any proportions>

so we assume that:

`p_1 =q_ 1= p_2 = q_2 = 0.5`

At confidence interval of 0.99 , the level of significance = 1 - 0.99 = 0.01

The critical value for
`z_(\alpha/2) = z_(0.01 /2)`

=
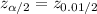
`z_(0.005)` = 2.576

The minimum sample size needed can be calculated by using the formula :

`n = (z^2_(\alpha/2))/(E^2)(p_1q_1+p_2q_2)`

`n = (2.576^2)/(0.06^2)((0.5 * 0.5)+(0.5 * 0.5))`

`n = (6.635776)/(0.0036)(0.25+0.25)`

`n =1843.271 * (0.5)`

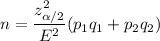
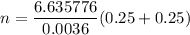
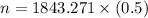
n = 921.63

n
`\simeq` 922

∴ The minimum sample size needed for each city = 922