Question

Use the Law of Sines to solve for all possible triangles that satisfy the given conditions. Below, enter your answers so that ∠A1 is smaller than ∠A2.)

a = 71, b = 104, ∠A = 21°
∠B1 = ∠B2 =
∠C1 = ∠C2 =
c1 = c2 =

Answer 1

`\angle B_(1) \approx 31.668^(\circ)`,
`\angle B_(2) \approx 148.332^(\circ)`

`\angle C_(1) \approx 127.332^(\circ)`,
`\angle C_(2) \approx 10.668^(\circ)`

`c_(1) \approx 157.532`,
`c_(2)\approx 36.676`

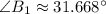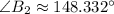
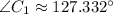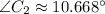
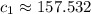Explanation:

The Law of Sines states that:

`(a)/(\sin A) = (b)/(\sin B)=(c)/(\sin C)`

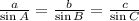
Where:

`a`,
`b`,
`c` - Side lengths, dimensionless.

`A`,
`B`,
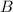`C` - Angles opposite to respective sides, dimensionless.

Given that
`a = 71`,
`b = 104`,
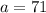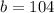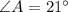`\angle A = 21^(\circ)`, the sine of angle B is:

`\sin B = (b)/(a)\cdot \sin A`

`\sin B = (104)/(71)\cdot \sin 21^(\circ)`

`\sin B = 0.525`

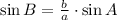
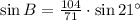
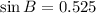
Sine is positive between 0º and 180º, so there are two possible solutions:

`\angle B_(1) \approx 31.668^(\circ)`

`\angle B_(2) \approx 148.332^(\circ)`

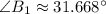
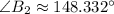
The remaining angle is obtained from the principle that sum of internal triangles equals to 180 degrees: (
`\angle A = 21^(\circ)`,
`\angle B_(1) \approx 31.668^(\circ)`,
`\angle B_(2) \approx 148.332^(\circ)`)

`\angle C_(1) = 180^(\circ)-\angle A - \angle B_(1)`

`\angle C_(1) = 180^(\circ)-21^(\circ)-31.668^(\circ)`

`\angle C_(1) \approx 127.332^(\circ)`

`\angle C_(2) = 180^(\circ)-\angle A - \angle B_(2)`

`\angle C_(2) = 180^(\circ)-21^(\circ)-148.332^(\circ)`

`\angle C_(2) \approx 10.668^(\circ)`

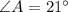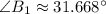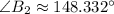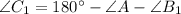
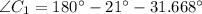
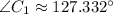
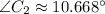
Lastly, the remaining side of the triangle is found by means of the Law of Sine: (
`a = 71`,
`\angle A = 21^(\circ)`,
`\angle C_(1) \approx 127.332^(\circ)`,
`\angle C_(2) \approx 10.668^(\circ)`)

`c_(1) = a\cdot \left((\sin C_(1))/(\sin A) \right)`

`c_(1) = 71\cdot \left((\sin 127.332^(\circ))/(\sin 21^(\circ)) \right)`

`c_(1) \approx 157.532`

`c_(2) = a\cdot \left((\sin C_(2))/(\sin A) \right)`

`c_(2)= 71\cdot \left((\sin 10.668^(\circ))/(\sin 21^(\circ)) \right)`

`c_(2)\approx 36.676`

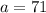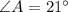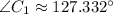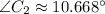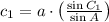
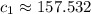
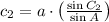
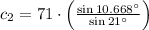
The answer are presented below:

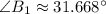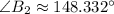
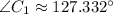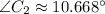
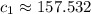`\angle B_(1) \approx 31.668^(\circ)`,
`\angle B_(2) \approx 148.332^(\circ)`

`\angle C_(1) \approx 127.332^(\circ)`,
`\angle C_(2) \approx 10.668^(\circ)`

`c_(1) \approx 157.532`,
`c_(2)\approx 36.676`