Question

A list of the top twenty restaurants in chicago was released. Four of the restaurants specialize in seafood. If five of the restaurants are selected randomly from the list, the standard deviation for the number of restaurants specializing in seafood is_____.

Answer 1

Answer: 0.7947...

Explanation:

The formula for the standard deviation of a hypergeometric distribution is:

`√(np (1-p) ) \sqrt{(N-n)/(N-1) }`

We are given:

- N (number of items in the population) = 20

- n (sample size) = 5

- s (population successes) = 4

Which means

- p = s/N = 4/20 = 0.2

So to plug in

`√(5*0.2(1-0.2))\sqrt{(20-5)/(20-1) }`

=0.7947194142... or just 0.7947

Answer 2

the standard deviation for the number of restaurants specializing in seafood is 0.8944

Explanation:

Given that :

Sum total number N of top restaurants in Chicago = 20

Four of the restaurants specialize in seafood,

then , the probability that a randomly selected restaurant from the top 20 in the list will specialize in seafood will be p = 4/20

p = 0.2

sample size n = 5

Assuming X to be the random variable that follows a Binomial distribution that represent the number of restaurants specializing in seafood.

Then:
`X \sim Binomial (n,p)`

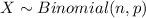
where;

n = 5 and p = 0.2

The standard deviation σ can be determined by using the formula:

`\sigma = √(np(1-p))`

`\sigma = √(5* 0.2(1-0.2))`

`\sigma = √(1.0(0.8))`

`\sigma = √(0.8)`

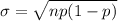
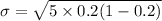
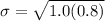
σ = 0.894427191

σ
`\simeq` 0.8944