Question

The time for service call follows a uniform distribution over the interval 20 to 60 minutes.

1. What is the probability that the service call takes longer than 30 minutes?
2. What is the interquartile range?
3. What is the 90th percentile?

Answer 1

(1) 0.75

(2) 30

(3) 56

Explanation:

Let X represent the time for service call.

It is provided that:
`X\sim Uni(20, 60)`

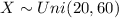
The probability density function of X is:

`f_(X)(x)=(1)/(b-a);\ a<X<b`

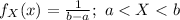
(1)

Compute the probability that the service call takes longer than 30 minutes as follows:

`P(X>30)=\int\limits^(60)_(30) {(1)/(60-20)} \, dx`

`=(1)/(40)* |x|^(60)_(30)\\\\=(60-30)/(40)\\\\=(3)/(4)\\\\=0.75`

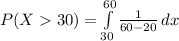
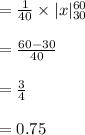
Thus, the probability that the service call takes longer than 30 minutes is 0.75.

(2)

The Inter quartile range is the difference between the 75th and 25th percentile.

From part (1), we know that P (X > 30) = 0.75.

⇒ 1 - P (X > 30) = 0.75

⇒ P (X < 30) = 0.25

The 25th percentile is 30.

Compute the 75th percentile as follows:

`P(X<x)=0.75\\\\\int\limits^(x)_(20) {(1)/(60-20)} \, dx=0.75\\\\(1)/(40)* |x|^(x)_(20)=0.75\\\\x-20=40* 0.75\\\\x=30+20\\\\x=50`

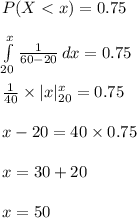
The 75th percentile is 50.

Then the inter quartile range is:

`IQR=P_(75)-P_(25)`

`=50-20\\=30`

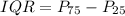
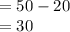
Thus, the inter quartile range is 30.

(3)

Compute the 90th percentile as follows:

`P(X<x)=0.90\\\\\int\limits^(x)_(20) {(1)/(60-20)} \, dx=0.90\\\\(1)/(40)* |x|^(x)_(20)=0.90\\\\x-20=40* 0.90\\\\x=36+20\\\\x=56`

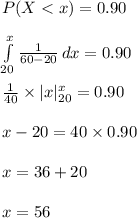
The 90th percentile is 56.