Answer:
Explained below.
Explanation:
(a)
It is provided that the price function for 1000 TVs is,
p (1000) = 400.
Also provided that if rebate of $10 is given then sale increases by 100 per week.
Let x be the number of unit sold per week then (x − 1000) is the increase in the number of units sold.
Then the price function is:
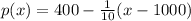

Thus, the demand function is,
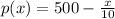 .
.
(b)
The revenue function is:
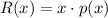
![=x[500-(x)/(10)]\\\\=500x-(x^(2))/(10)](https://img.qammunity.org/2021/formulas/mathematics/college/dbr8jwf6y6qlsovuc5e4nt0emduodi5o5v.png)
Maximize the revenue as follows:
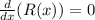
![(d)/(dx)[500x-(x^(2))/(10)]=0](https://img.qammunity.org/2021/formulas/mathematics/college/8gja2kftls8va6mw9rc9t8570nqr5wtp8n.png)
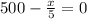

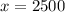
Observe that R'(x) > 0 for 0 ≤ x < 2500 and R'(x) < 0 for x > 2500. Hence, first derivative test will lead to the conclusion that maximum occurs at x = 2500.
Compute the value p (2500) as follows:

Then the rebate to maximize the revenue should be: $400 - $250 = $150.
(c)
The weekly cost function is,
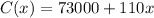
Compute the profit function as follows:

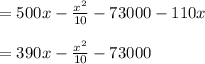
Compute the marginal profit as follows:
![\text{Marginal profit}=P'(x)\\=(d)/(dx)P(x)\\=(d)/(dx)[390x-(x^(2))/(10)- 73000]\\=390-(x)/(5)](https://img.qammunity.org/2021/formulas/mathematics/college/peof12nl9u7lm5x5rvkuaamdy024sosnrp.png)
Compute the value of x for P'(x) = 0 as follows:
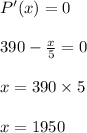
Observe that P'(x) > 0 for 0 ≤ x < 1950 and P'(x) < 0 for x > 1950. Hence, first
derivative test will lead to the conclusion that maximum occurs at x = 1950.
Compute the value p (1950) as follows:
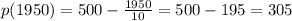
Then the rebate to maximize the profit should be: $400 - $305 = $95.