Question

The average heights of x number of girls and 15 boys is 123. if the average heights of boys is 125 and that of girls is 120.find number of girls.​

Answer 1

`x = 10`. In other words, there number of girls is
`10`.

Explanation:

The average of a number of measurements is equal to the sum of these measurements over the number of measurements.

`\displaystyle \text{Average} = \frac{\text{Sum of measurements}}{\text{Number of measurements}}`.

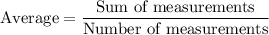Rewrite to obtain:

`\begin{aligned}& \text{Sum of measurements}= (\text{Number of measurements}) * (\text{Average}) \end{aligned}`.

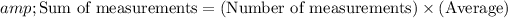For this question:

`\begin{aligned}& \text{Sum of heights of boys} \\ &= (\text{Number of boys}) * (\text{Average height of boys}) \\ &= 15 * 125 = 1875\end{aligned}`.

`\begin{aligned}& \text{Sum of heights of girls} \\ &= (\text{Number of girls}) * (\text{Average height of girls}) \\ &= x * 120 = 120\, x\end{aligned}`.

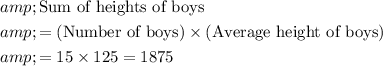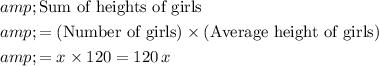Therefore:

`\begin{aligned}& \text{Sum of boys and girls} \\ &= \text{Sum of heights of boys} + \text{Sum of heights of girls}\\ &= 1875 + 120\, x\end{aligned}`.

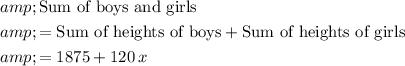On the other hand, there are
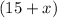`(15 + x)` boys and girls in total. Using the formula for average:

`\begin{aligned}& \text{Average height of boys and girls} \\ &= \frac{\text{Sum of heights of boys and girls}}{\text{Number of boys and girls}} \\ &= (1875 + 120\, x)/(15 + x)\end{aligned}`.

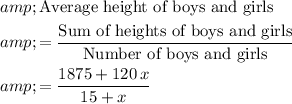From the question, this average should be equal to
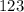`123`. In other words:

`\displaystyle (1875 + 120\, x)/(15 + x) = 123`.

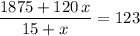Solve this equation for
`x` to obtain:

`1875 + 120\, x= 123\, (15 + x)`.

`(123 - 120)\, x = 1875 - 123 * 15`.

`x = 10`.

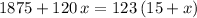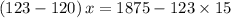In other words, the number of girls here is
`10`.