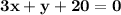Question

Write the equation of the line in standard form

64. contains (-8, 4)
and the midpoint of the
segment connecting
(-10, 5) and (-5, 0). Show your work.

Answer 1

`\bold{3x+y+20=0}`

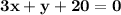
Explanation:

Mid point of (-10, 5) and (-5, 0).

Other point (-8, 4).

To find:

Equation of line in standard form that connect the mid point and other point.

Solution:

Mid point formula is given as:

`x = (x_1+x_2)/(2)\\y = (y_1+y_2)/(2)`

`x = (-10+-5)/(2) = -7.5\\y = (5+0)/(2) = 2.5`

Now, the two points are: (-7.5, 2.5) and (-8, 4)

Slope intercept form of line is given as:

`y = mx+c`

`m=(4-2.5)/(-8-(-7.5)) = -3`

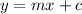
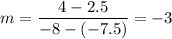
So, the equation of line is:

`\Rightarrow y =-3x+c`

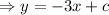
Putting (-8, 4) to find c:

`4=-3* -8+c\\\Rightarrow c = -20`

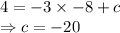
Equation of line:

`\Rightarrow y =-3x-20`

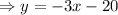
In standard form:

`\bold{3x+y+20=0}`