Question

Given that (y+2), (y+3)and (2y^2+1) are consecutive terms of an arithmetic progression find the value of x

Answer 1

In an arithmetic sequence, the difference between any consecutive terms should be always the same, then we have:

(y + 3) - (y + 2) = D

(2*y^2 + 1) - (y + 3) = D.

From the first equation, we can find the value of D:

y + 3 - y - 2 = D

1 = D.

Replacing this in the second equation, we have:

(2*y^2 + 1) - (y + 3) = 1

Now we can solve this equation:

2*y^2 + 1 - y - 3 - 1 = 0

2*y^2 - y - 3 = 0.

The solutions of this quadratic equation can be found with the Bhaskara's equation:

`y = (1 +- √(1^2 - 4*2*(-3)) )/(2*2) = (1+-√(25) )/(4) = (1+-5)/(4)`

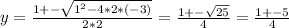
Then the possible values of y are:

y = (1 + 5)/4 = 6/4

y = (1 - 5)/4 = -1