Question

Solve application problems using quadratic equations. A positive real number is 4 less than another. If the sum of the squares of the two numbers is 72, then find the numbers.

Answer 1

Hello, let's note a this positive real number.

The sum of the square is

`a^2+(a-4)^2`

right?

So, we need to solve

`a^2+(a-4)^2=72`

We will develop, simplify.

Let's do it!

`a^2+(a-4)^2=72\\\\a^2+a^2-8a+16=72\\\\2a^2-8a+16-72=0\\\\2(a^2-4a-28)=0\\\\a^2-4a-28=0`

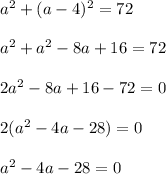
Now, we can use several methods to move forward. Let's complete the square.

`a^2-4a=a^2-2*2*a=(a-2)^2-2^2=(a-2)^2-4`

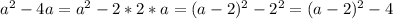
So,

`a^2-4a-28=0\\\\(a-2)^2-4-28=0\\\\(a-2)^2=32=4^2*2\\\\a-2=\pm4√(2)\\\\a = 2(1+2√(2)) \ \ or \ \ a = 2(1-2√(2))`

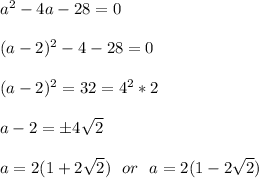
As a should be positive, the solution is

`\Large \boxed{\sf \bf \ \ a = 2(1+2√(2)) \ \ }`

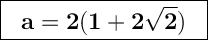
and the other number is

`2(1+2√(2))-4=2(2√(2)-1)`

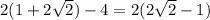
Thank you.