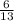Answer:
p =
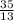 and q =
and q =
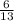
Explanation:
Given equations:
2p - 3q = 4 -----------(i)
3p + 2q = 9 ------------(ii)
Let's solve this equation simultaneously using the elimination method
(a) Multiply equation (i) by 3 and equation (ii) by 2 as follows;
[2p - 3q = 4] x 3
[3p + 2q = 9] x 2
6p - 9q = 12 -------------(iii)
6p + 4q = 18 -------------(iv)
(b) Next, subtract equation (iv) from equation (iii) as follows;
[6p - 9q = 12]
- [6p + 4q = 18]
-13q = -6 -----------------(v)
(c) Next, make q subject of the formula in equation (v)
q =
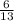
(d) Now substitute the value of q =
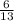 into equation (i) as follows;
into equation (i) as follows;
2p - 3(
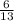 ) = 4
) = 4
(e) Now, solve for p in d above
Multiply through by 13;
26p - 18 = 52
Collect like terms
26p = 52 + 18
26p = 70
Divide both sides by 2
13p = 35
p =
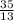
Therefore, p =
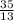 and q =
and q =