Question

Given that (y+z), (y+3) and (2y^2-1) are consecutive terms of an arithmetic progression. Find the possible values of y

Answer 1

This problem actually says:

(y + 2), (y + 3) and (2*y^2 - 1) are consecutive terms of an arithmetic progression.

Now, the difference between two consecutive terms in an arithmetic progression is always the same, so we have:

(y + 3) - (y +2) = D

(2*y^2 - 1) - (y + 3) = D

From the first equation we have:

y + 3 - y - 2 = 1 = D

Now we can replace it in the other equation:

2*y^2 - 1 - y - 3 = 1

2*y^2 - y - 5 = 0

Now we need to solve that equation to find the possible values of y.

To solve a quadratic equation of the form:

a*x^2 + b*x + c = 0, we can use the Bhaskara's equation:

`y = (-b +- √(b^2 -4*a*c) )/(2*a)`

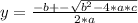
in this case, the solutions are:

`y = \frac{1 +-\sqrt[]{(-1)^2 - 4*2*(-5)} }{2*2} = (1 +- √(61) )/(4) = (1+-6.4)/(4)`

Then the possible values of y are:

y = (1 + 6.4)/4 = 1.85

y = (1 - 6.4)/5 = -1.35