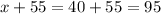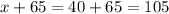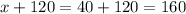Answer:
40°, 95°, 105°, and 160°
Explanation:
Let the smallest angle be x.
Measures of the 3 angles can be expressed as:
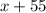
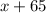
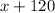
The sum of all angles in a quadrilateral = 360°.
Therefore,
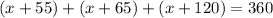
Solve for x
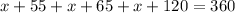
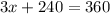
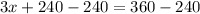
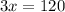
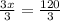
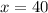
The smallest angle = 40°
Plug in the value of x in the earlier stated expressions to find the measure of the other angles: