Question

A ladder 10 m long,leans against a vertical wall at an angle of 70° to the ground.if the ladder slips down the wall 4m,find,correct to 2 significant figure

(a) the new angle which the ladder makes with the ground

(b) the distance the ladder slipped back on the ground from it's original position
​

Answer 1

Answer to part (a) is: 33 degrees

Answer to part (b) is: 5 meters

=============================================

Step-by-step explanation:

Check out the diagram below.

For now, focus only on triangle ABC. The ladder is segment AC = 10. We first need to find the length of
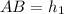`AB = h_1` which is the initial height of the ladder.

sin(angle) = opposite/hypotenuse

sin(70) = h/10

h = 10*sin(70)

h = 9.396926 approximately

Subtract off 4 since the ladder slips 4 meters down the wall

h-4 = 9.396926-4

h-4 = 5.396926

which is the new height the ladder reaches. The hypotenuse stays the same

sin(angle) = opposite/hypotenuse

sin(theta) = 5.396926/10

theta = arcsin(5.396926/10)

theta = 32.662715

theta = 33 degrees when rounding to 2 significant figures

This is the value of
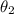`\theta_2` in the diagram below.

---------------------------------

We'll use the cosine rule with the old theta value
`\theta_1`

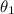
cos(angle) = adjacent/hypotenuse

cos(70) = x/10

x = 10*cos(70)

x = 3.420201 is the approximate distance the foot of the ladder is from the wall. This is before the ladder slips.

After the ladder slips, we use the new angle value
`\theta_2`

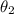
cos(angle) = adjacent/hypotenuse

cos(32.662715) = x/10

x = 10*cos(32.662715)

x = 8.418622

Subtract the two x values

8.418622-3.420201 = 4.998421

which gives the approximate distance the foot of the ladder moved (the distance from point C to point E in the diagram)

This rounds to 5.0 or simply 5 when rounding to 2 significant figures.