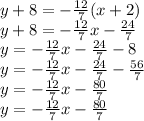Question

Write the equation of the line in slope intercept form that passes through (-2, -8) and (-9, 4)

Please provide steps to solve if possible

Answer 1

`y=-(12)/(7)x-(80)/(7)`

Explanation:

In order to find the slope-intercept form of a line when given two points, we need to first put it into point-slope form. The point-slope form is given by the equation:

`y-y_1=m(x-x_1)`

Where m is the slope and x₁ and y₁ is one of the two points.

Anyways, let's first find the slope. Let's designate (-2,-8) as x₁ and y₁ and (-9,4) as x₂ and y₂ (it doesn't really matter). The formula for slope is:

`m=(y_2-y_1)/(x_2-x_1) =((4)-(-8))/((-9)-(-2))=12/-7=-12/7`

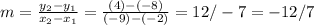
So, the slope is -12/7.

Now, pick a point for the point-slope form. To keep things consistent, I'm going to use the point (-2,-8) as x₁ and y₁. Plug in -12/7 for m. Therefore:

`y-(-8)=-(12)/(7)(x-(-2))\\`

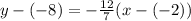
Now, simplify, distribute, and isolate the y:

`y+8=-(12)/(7)(x+2)\\y+8=-(12)/(7)x-(24)/(7)\\y=-(12)/(7)x-(24)/(7)-8\\y=-(12)/(7)x-(24)/(7)-(56)/(7) \\y=-(12)/(7)x-(80)/(7)\\y=-(12)/(7)x-(80)/(7)`