Answer:
Please see steps below
Explanation:
Start by writing all trig functions in the equation in terms of their simplest forms using the two basic trig functions:
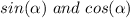 :
:
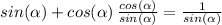
Now work on the left side (which is the most complicated one), trying to simplify it using the properties for adding fractions with different denominators:
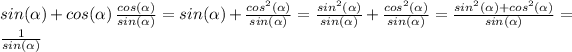
where in the last step we have used that the Pythagorean identity for:
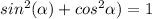
Notice that we arrived at the expression:
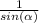 , which is exactly what appears on the other side of the initial equation/identity we needed to prove, so the prove has been completed.
, which is exactly what appears on the other side of the initial equation/identity we needed to prove, so the prove has been completed.