Answer:
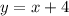
Explanation:
Two parallel lines will have the same slope:
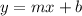
This is the y-intercept equation, where m is the slope and b is the y-intercept:
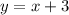
The slope is x, or 1x, so the parallel line is also x.
Find the y-intercept:
You do this by taking the equation given and solving for y:
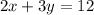
Isolate the variable y. Subtract 2x from both sides:
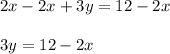
Isolate y by dividing both sides by 3:
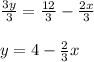
Rearrange in slope-intercept form:
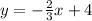
The y-intercept of this equation is 4.
Now make the equation using the given information:
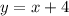
:Done