Question

Logx - logx-1^2=2log(x-1)

Answer 1

x is approximately 2.220744

Explanation:

This can be simplified a little using properties of logarithms, and then solve it by graphing:

`log(x)-log(x-1)^2=2\,log(x-1)\\log(x)-2\,log(x-1)=2\,log(x-1)\\log(x)=4\,log(x-1)`

So we use a graphing tool to find the intersection point of the graph of
`log(x)`, and the graph of
`4\,log(x-1)`

Please see attached image for the graph and solution.

The value of x is approximately 2.220744

Answer 2

x = 2.32011574011

Explanation:

The problem with your original equation is that it is a long way of saying ...

log(x) -log(x) -1 = 2log(x-1)

0 -1 = 2log(x-1)

which has the solution ...

-1/2 = log(x -1)

1/√10 = x -1

x = 1 + 1/√10 ≈ 1.3162278

__

We have asked for clarification, and what we got was ...

`\log{(x)}-\log{(x-1^2)}=2\log{(x-1)}`

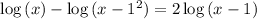
which, again, is a long way of saying ...

`\log{(x)}-\log{(x-1)}=2\log{(x-1)}`

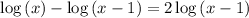
The other reasonable interpretation of your 'clarified' equation is ...

`\log{(x)}-\log{((x-1)^2)}=2\log{(x-1)}`

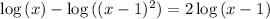
which you already have an answer to. You have declared that a "misconception."

So, we are left with the interpretation that the equation you want a solution to is ...

`\log{(x)}-\log{(x-1)}=2\log{(x-1)}`

_____

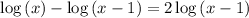
When solving these graphically, I like to write the equation as a function whose zero(s) we're trying to find. For this, when we subtract the right side, we get ...

`f(x)=\log{(x)}-3\log{(x-1)}`

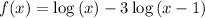
A graphing calculator shows that f(x) = 0 when ...

x ≈ 2.32011574011

__

If you don't like my interpretation, check out the second attachment. It has your x-1² as the argument of the middle term. You can see that the calculator interpreted that the same way I did (as required by the order of operations).