Answer:
The equation has the solution(s) x = - 5, and x = 2
Explanation:
Let's start by adding log(10) to either side of the equation --- (1)

=
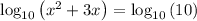
If you recall, one property proves that
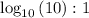 . We can substitute this value back into the simplified equation --- (2)
. We can substitute this value back into the simplified equation --- (2)
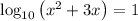
We can also apply the logarithmic definition, If logₐ(b) = c then b = aᶜ. Using this definition we receive a further simplified equation --- (3)
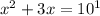
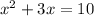
Solving for the expression we receive the solution(s) x = 2, and x = - 5, our first option.
Note : The first solution is correct, but I wanted to take a slightly different approach