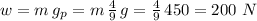Question

A body weights 450 N on the surface of Earth . How much will it weigh on the surface of a planet whose masss is 1/9th mass of Earth and radius is half of radius of Earth?​

Answer 1

The weight of the body on the other planet would be 200 N

Step-by-step explanation:

Recall that the acceleration of gravity at sea level on Earth is obtained via the general Gravitational force formula when the distance "d" is the radius of the Earth (R):

`F=m\,g=G\,(m\,\,m_E)/(R^2) = m \,(G\,(m_E)/(R^2) )`

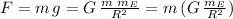
We are told that the weight of the object on Earth is 450 N, that is:

`W=m\,g= m \,(G\,(m_E)/(R^2) )= 450`

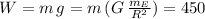
in this other planet the acceleration of gravity will be different as shown below:

`(G\,(m_E\,(1/9))/((R/2))^2) )=(G\,(m_E\,\,4)/(R^2\,\,9) )=(4)/(9) (G\,(m_E)/(R^2) )`

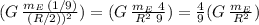
so, its gravity is 4/9 that of the Earth, which now we can use to convert its weight (w) on the planet as 4/9 the weight it has on Earth:

`w=m\,g_p=m\,(4)/(9) \,g=(4)/(9) \,450= 200\,\, N`