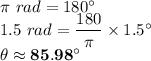Question

Bryan drives up to a traffic circle from Elm Street. He drives 15 meters around the circle is a perfect circle with a radius of 10 meters, at what angle is Maple Street to Elm Street?

Answer 1

`\approx \bold{85.98^\circ}`

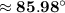
Explanation:

Given that

Radius of circle = 10 metres

Bryan drives 15 metres around the circle.

To find:

The angle of Maple street to Elm street = ?

Solution:

Kindly refer to the image attached.

The Elm street meets the circle at A.

Maple street at B.

Given that arc length AB = 15m

Radius of circle = 10 m

We have to find the angle of arc.

Let us use the formula:

`\theta = (l)/(r)\\\Rightarrow \theta = (15)/(10) \\\Rightarrow \bold{\theta = 1.5\ radians}`

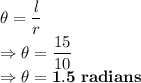
Converting to degrees:

`\pi\ rad = 180^\circ\\1.5\ rad = (180)/(\pi) * 1.5^\circ\\\theta \approx \bold{85.98^\circ}`

Answer 2

85.9°

Explanation:

Using the formula for calculating the length of an arc to get the angle of Maple Street to Elm Street;

Length of an arc = θ/360 * 2Πr where r is the radius of the circle.

Given r = 10m and length of the arc = 15m

On substituting;

15 = θ/360 * 2π(10)

15 = θ/360 * 20π

θ/360 = 15/20π

θ/360 = 0.2387

θ = 360* 0.2387

θ = 85.9°

Hence Maple street is at 85.9° to Elm street.