Question

Pick out the set of numbers that is not Pythagorean triple

9 40 46
16 30 34
10 24 26
50 120 130

Answer 1

Option A is the correct option.

Explanation:

1. Let h , p and b are the hypotenuse , perpendicular and base of a right - angled triangle respectively.

From Pythagoras theorem,

`\sf{ {h}^(2) = {p}^(2) + {b}^(2) }`

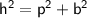
Here, we know that the hypotenuse is always greater than perpendicular and base,

h = 46 , p = 40 , b = 9

⇒
`\sf{ {46}^(2) = {40}^(2) + {9}^(2) }`

⇒
`2116 = 1600 + 81`

⇒
`\sf{2116  ≠ 1681}`

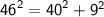
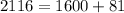
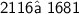
Thus , the relation
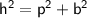`\sf{ {h}^(2) = {p}^(2) + {b}^(2) }` is not satisfied by h = 46 , p = 40 , b = 9

So, The set of numbers 9 , 40 , 46 is not Pythagorean triple.

------------------------------------------------------

2. 16 , 30 , 34

h = 34 , p = 30 , b = 16

`\sf{ {h}^(2) = {p}^(2) + {b}^(2) }`

⇒
`\sf{ {34}^(2) = {30}^(2) + {16}^(2) }`

⇒
`\sf{1156 = 900 + 256}`

⇒
`\sf{1156 = 1156}`

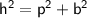
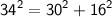
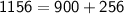
The relation
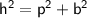`\sf{ {h}^(2) = {p}^(2) + {b}^(2) }` is satisfied by the particular values of h , p and b i.e h = 34 , p = 30 , b = 16

So, the set of numbers 16 , 30 , 34 is a Pythagorean triple.

------------------------------------------------------

3. 10, 24 , 26

h = 26 , p = 24 , b = 10

`\sf{ {h}^(2) = {p}^(2) + {b}^(2) }`

⇒
`\sf{ {26}^(2) = {24}^(2) + {10}^(2) }`

⇒
`\sf{676 = 576 + 100}`

⇒
`\sf{676 = 676}`

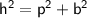
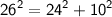
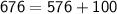
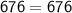
The relation
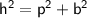`\sf{ {h}^(2) = {p}^(2) + {b}^(2) }` is satisfied by the particular values of h , p and h i.e h = 26 , p = 24 , b = 10

So, the set of numbers 10, 24 , 26 is the Pythagorean triple.

-----------------------------------------------------

4. 50 , 120 , 130

h = 130 , p = 120 , b = 50

`\sf{ {h}^(2) = {p}^(2) + {b}^(2) }`

⇒
`\sf{ {130}^(2) = {120}^(2) + {50}^(2) }`

⇒
`\sf{16900 = 14400 + 2500}`

⇒
`\sf{16900 = 16900}`

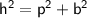
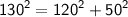
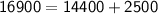
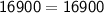
The relation
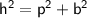`\sf{ {h}^(2) = {p}^(2) + {b}^(2) }` is satisfied by the particular values of h , p and b i.e h = 130 , p = 120 , b = 50

So, the set of numbers 50, 120 , 130 is the Pythagorean triple.

-----------------------------------------------------

In this way, to satisfy the Pythagoras Theorem , the hypotenuse ( h ) , perpendicular ( p ) and the base ( b ) of a right - angles triangle should have the particular values in order. These values of h , p and b are called Pythagorean triple.

Hope I helped!

Best regards!!

Answer 2

`\huge\boxed{9,40,46}`

Explanation:

Let's check it using Pythagorean Theorem:

`c^2 = a^2 + b^2`

Where c is the longest sides, a and b are rest of the 2 sides

1) 9 , 40 , 46

=>
`c^2 = a^2 + b^2`

=>
`46^2 = 9^2 + 40^2`

=> 2116 = 81 + 1600

=> 2116 ≠ 1681

So, this is not a Pythagorean Triplet

2) 16, 30 and 34

=>
`c^2 = a^2 + b^2`

=>
`34^2 = 16^2 + 30^2`

=> 1156 = 256 + 900

=> 1156 = 1156

No need to check more as we've found the one which is not a Pythagorean Triplet.