Answer:
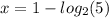
Explanation:
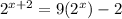
Using the rules of indices
That's
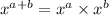
So we have

So we have
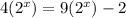
Let
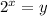
We have
4y = 9y - 2
4y - 9y = - 2
- 5y = - 2
Divide both sides by - 5
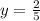
But
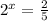
Take logarithm to base 2 to both sides
That's
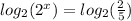
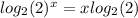

So we have
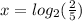
Using the rules of logarithms
That's
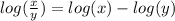
Rewrite the expression
That's
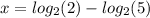
But

So we have the final answer as
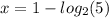
Hope this helps you