Question

PLEASE ASAP! I SENT A PHOTO CHECK AND TELL!

Answer 1

Answer B is the correct answer: "Motion of one projectile as seen from the other is a straight line."

Step-by-step explanation:

Let's write the equations of motion for each projectile, using that projectile
`a` is launched with velocity
`a` which has components associated with the angle of launching, given in x and y coordinates as:
`a_x\,\,and\,\,a_y`.

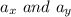Similarly, assume that projectile b is launched with velocity
`b` with components due to the launching angle =
`b_x\,\,and \,\,b_y`

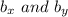
then the equations of motion for the two projectiles launched at the same time (t) from the same spot (position that we assume to be at the origin of coordinates to simplify formulas) are:

`x_a=a_x\,t\\y_a= a_y\,t-(1)/(2) g\,t^2\\and\\x_b=b_x\,t\\y_b= b_y\,t-(1)/(2) g\,t^2`

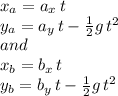
therefore, from the frame of reference of projectile "b", the x and y position of projectile "
`a`" would be:

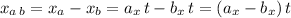`x_(a\,b)= x_a-x_b= a_x\,t-b_x\,t=(a_x-b_x)\,t` which is linear in "t"

`y_(a\,\,b)=y_a-y_b= a_y\,t-(1)/(2) g\,t^2-\left[ b_y\,t-(1)/(2) g\,t^2\right]=(a_y-b_y)\,t` which is also linear in t.

Therefore the motion of one projectile with reference to the other is a straight line (answer B)

Notice as well that this two projectiles cannot collide because they have been launched together, and supposedly at different speeds and angles. The only way that they can share the same x-coordinate and the same y-coordinate at the same time "t" is if their velocity components are equal, which is not what we are told.

`x_a=x_b\\a_x\,t= b_x\,t\\and\\y_a= y_b\\a_y\,t-(1)/(2) g\,t^2= b_y\,t-(1)/(2) g\,t^2\\a_y\,t=b_y\,t\\a_y=b_y`