Question

What is the volume of a sphere with a diameter of 12 cm.

Answer 1

Volume of sphere by formula is V= 4/3πr^3

Since d= 12

Then r = d/2

Radius = diameter / 2

r = 12/2

r = 6

V = 4/3 x 22/7 x 6^3

V = 1.33 x 3.14 x 216

V = 902.1cm^3....

Thanks

Answer 2

288π cm³, 904.32 cm³, and 904.778683 cm³

Explanation:

The volume of a sphere can be found using the following formula.

`V=(4)/(3) \pi r^3`

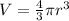
We are given the diameter, so we must find the radius.

The radius is half of the diameter.

r= d/2

The diameter is 12 cm.

r= 12 cm/2

r= 6 cm

The radius is 6 centimeters. Let's return to the formula and substitute 6 cm in for r.

`V=(4)/(3) \pi (6cm)^3`

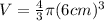
Evaluate the exponent.

`(6 cm)^3= 6 cm * 6 cm * 6cm = 36 cm^2 * 6cm= 216 cm^3`

`V=(4)/(3) \pi * 216 cm^3`

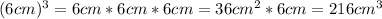
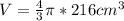
Multiply 4/3 and 216 cm^3

`V= ((4)/(3) * 216 cm^3)\pi`

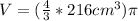
In terms of pi:

`V= 288\pi cm^3`

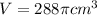
Using 3.14 as pi:

`V= 288 \pi cm^3`

`V= (288 * 3.14) cm^3`

`V= 904.32 cm^3`

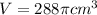
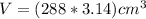
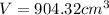
Using 3.14159265 as pi:

`V= 288 \pi cm^3`

`V= (288 * 3.14159265) cm^3`

`V=904.778683 cm^3`

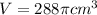
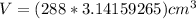
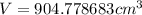
The volume of the sphere is 288π cm³, 904.32 cm³, and 904.778683 cm³