Question

Let $a \bowtie b = a+\sqrt{b+\sqrt{b+\sqrt{b+...}}}$. If $7\bowtie g = 9$, find the value of

Answer 1

Answer: g = 2

================================================

Work Shown:

`a \bowtie b = a + \sqrt{b+\sqrt{b+√(b+...)}}\\\\7 \bowtie g = 7 + \sqrt{g+\sqrt{g+√(g+...)}} = 9\\\\\sqrt{g+\sqrt{g+√(g+...)}} = 2`

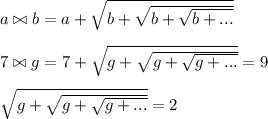
After subtracting 7 from both sides.

Note how because we have an infinite sequence of nested radicals, we can let
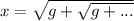`x = \sqrt{g+√(g+...)}` which means x is equal to 2 as well.

This lets us say

`\sqrt{g+\sqrt{g+√(g+...)}} = √(g+x) = x`

Solve the equation
`√(g+x)= x` for x to get

`√(g+x) = x\\\\g+x = x^2\\\\x^2-x-g = 0\\\\x = (-b\pm√(b^2-4ac))/(2a)\\\\x = (-(-1)\pm√((-1)^2-4(1)(-g)))/(2(1))\\\\x = (1\pm√(1+4g))/(2)\\\\x = (1+√(1+4g))/(2) \ \text{ or } \ x = (1-√(1+4g))/(2)`

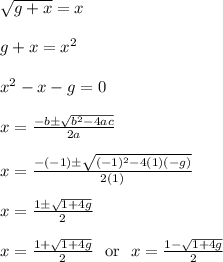
Since x is positive, this means we only focus on the first equation in the last line above.

Earlier we let x be equal to the infinite nested radicals involving g, but x is also equal to 2. So plug in x = 2 and use that to find g.

`x = (1+√(1+4g))/(2)\\\\2 = (1+√(1+4g))/(2)\\\\4 = 1+√(1+4g)\\\\3 = √(1+4g)\\\\9 = 1+4g\\\\1+4g = 9\\\\4g = 8\\\\g = 2\\\\`

As a check, we can do the following

`7 + \sqrt{2+√(2)} \approx 8.84775906502258\\\\7 + \sqrt{2+\sqrt{2+√(2)}} \approx 8.96157056080647\\\\7 + \sqrt{2+\sqrt{2+\sqrt{2+√(2)}}} \approx 8.9903694533444\\\\`

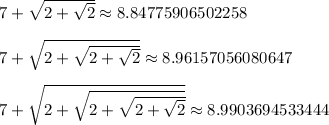
we're slowly approaching 9

Answer 2

Answer:
`g = \boxed{2}`

Explanation:

`\sqrt{g+\sqrt{g+√(g+...)}}=2`

implies that

`\sqrt{g+\sqrt{g+√(g+...)}}=√(g+2)=2`.

Squaring both sides of this new equality, we have
`g + 2 = 4 \implies g = \boxed{2}`