Answer: x = 10 is the positive root
================================================
Work Shown:
First get everything to one side
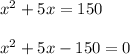
Now use the quadratic formula
Plug in a = 1, b = 5, c = -150.

Factoring, completing the square, or graphing are alternative methods to get these two answers. We see that the positive root is x = 10.