Answer: y=23
Explanation:
If Points and A,B and C lines on the same line then they will have the same slopes so since we have the coordinates of A and B we will use the to write an equation in slope intercept form.
To write it in slope intercept form we will need to find the slope and the y intercept.
To find the slope you will find the change in the y coordinates and divide it by the change in the x coordinates.
Using the coordinates (-1,7) and (2,19) the y coordinates are 7 and 19 and the x coordinates are -1 and 2.
Slope :
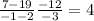 In this case the slope is 4 so we will use that to find the y intercept by using point A coordinate.
In this case the slope is 4 so we will use that to find the y intercept by using point A coordinate.
The slope intercept formula says that y=mx +b where me is the slope and b is the y intercept.
7=4(-1) + b
7 = -4 + b
+4 +4
b= 11 The y intercept is 11.
Now we can write the whole equation as y=4x + 11 .
To answer the question now, where we need to find y , we will plot the x coordinate which is 3 into the equation and solve for y.
y = 4(3) + 11
y = 12 + 11
y = 23