Answer:
Correct option is length = 4, width = 3.
Explanation:
Given:
Diagonal of a rectangle is rational.
To find:
Which of the following length and width options represent a rectangle ?
options:
length = 2, width = 1
length = 4, width = 4
length = 3, width = 2
length = 4, width = 3
Solution:
First of all, let us consider a rectangle as shown in the attached answer image.
Rectangle ABCD.
Width of rectangle is AB.
Width of rectangle is BC.
And the diagonal AC or BD can be found by using Pythagorean Theorem:
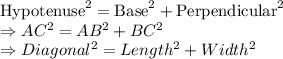
Now, let us find diagonal for each option and check whether it is rational or not.
Option 1:
length = 2, width = 1
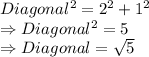
Not rational
Option 2:
length = 4, width = 4
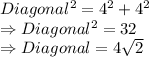
Not rational.
Option 3:
length = 3, width = 2
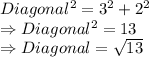
Not rational.
Option 4:
length = 4, width = 3
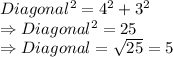
Diagonal is rational.
Correct option is length = 4, width = 3.