Question

Complete parts ​(a) through ​(c) below. ​(a) Determine the critical​ value(s) for a​ right-tailed test of a population mean at the level of significance with degrees of freedom. ​(b) Determine the critical​ value(s) for a​ left-tailed test of a population mean at the level of significance based on a sample size of n. ​(c) Determine the critical​ value(s) for a​ two-tailed test of a population mean at the level of significance based on a sample size of n.

Answer 1

(a) The critical value of t at P = 0.01 and 15 degrees of freedom is 2.602.

(b) The critical value of t at P = 0.05 and 19 degrees of freedom is -1.729.

(c) The critical value of t at P = 0.025 and 12 degrees of freedom is -2.179 and 2.179.

Explanation:

We have to find the critical t values for each of the following levels of significance and sample sizes given below.

As we know that in the t table there are two columns. The horizontal column is represented by the symbol P which represents the level of significance and the vertical column is represented by the symbol '
`\\u`' which represents the degrees of freedom.

(a) A right-tailed test of a population mean at the α=0.01 level of significance with 15 degrees of freedom.

So, here the level of significance = 0.01

And the degrees of freedom = n - 1 = 15

Now, in the t table, the critical value of t at P = 0.01 and 15 degrees of freedom is 2.602.

(b) A left-tailed test of a population mean at the α=0.05 level of significance with a sample size of n = 20.

So, here the level of significance = 0.05

And the degrees of freedom = n - 1

= 20 - 1 = 19

Now, in the t table, the critical value of t at P = 0.05 and 19 degrees of freedom is -1.729.

(c) A two-tailed test of a population mean at the α=0.05 level of significance with a sample size of n = 13.

So, here the level of significance =
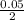`(0.05)/(2)` = 0.025 {for the two-tailed test}

And the degrees of freedom = n - 1

= 13 - 1 = 12

Now, in the t table, the critical value of t at P = 0.025 and 12 degrees of freedom is -2.179 and 2.179.