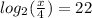Question

If Log 4 (x) = 12, then log 2 (x / 4) is equal to A. 11 B. 48 C. -12 D. 22

Answer 1

`\huge \boxed{\mathrm{D. \ 22}}`

Explanation:

`\mathrm{log_4 (x)=12}`

Make the base 4 from both sides.

`\mathrm{4^(log_4 (x))=4^(12)}`

Simplify the equation.

`\mathrm{x=16777216}`

`\mathrm{log_2 ((x)/(4) )}`

Let x = 16777216

`\mathrm{log_2 ((16777216)/(4) )}`

`\mathrm{log_2 (4194304)}`

Evaluate.

`22`

Answer 2

`log_2((x)/(4) )=22`

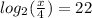
which is your answer "D"

Explanation:

If
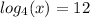`log_4(x)=12` this means that :
`x=4^(12)` based in the definition of logarithm.

And this exponential expression can also be written using that
`4=2^2`:

`x=4^(12)=(2^2)^(12)=2^(24)`

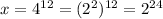
so now we know what x is with base 2 (which is needed for the second expression:

`log_2((x)/(4) )=?`

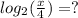
And this also can be written in exponent form (using the unknown "?" we need to find) as:

`2^?=(x)/(4) \\x=4\,*\,2^?\\x=2^2\,*\,2^?\\x=2^(2+?)`

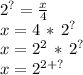
Since we know the value of x in base 2 (from our first analysis), then:

`x=2^(2+?)=2^(24)\\then\\2+?=24\\?=22`

Therefore,

`log_2((x)/(4) )=22`