Question

If vectors i+j+2k, i+pj+5k and 5i+3j+4k are linearly dependent, the value of p is what?​

Answer 1

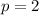`p = 2` if given vectors must be linearly independent.

Explanation:

A linear combination is linearly dependent if and only if there is at least one coefficient equal to zero. If
`\vec u = (1,1,2)`,
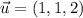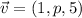`\vec v = (1,p,5)` and
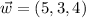`\vec w = (5,3,4)`, the linear combination is:

`\alpha_(1)\cdot (1,1,2)+\alpha_(2)\cdot (1,p,5)+\alpha_(3)\cdot (5,3,4) =(0,0,0)`

In other words, the following system of equations must be satisfied:

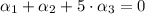`\alpha_(1)+\alpha_(2)+5\cdot \alpha_(3)=0` (Eq. 1)

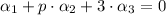`\alpha_(1)+p\cdot \alpha_(2)+3\cdot \alpha_(3)=0` (Eq. 2)

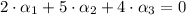`2\cdot \alpha_(1)+5\cdot \alpha_(2)+4\cdot \alpha_(3)=0` (Eq. 3)

By Eq. 1:

`\alpha_(1) = -\alpha_(2)-5\cdot \alpha_(3)`

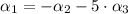
Eq. 1 in Eqs. 2-3:

`-\alpha_(2)-5\cdot \alpha_(3)+p\cdot \alpha_(2)+3\cdot \alpha_(3)=0`

`-2\cdot \alpha_(2)-10\cdot \alpha_(3)+5\cdot \alpha_(2)+4\cdot \alpha_(3)=0`

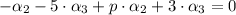
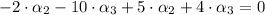
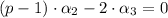`(p-1)\cdot \alpha_(2)-2\cdot \alpha_(3)=0` (Eq. 2b)

`3\cdot \alpha_(2)-6\cdot \alpha_(3) = 0` (Eq. 3b)

By Eq. 3b:

`\alpha_(3) = (1)/(2)\cdot \alpha_(2)`

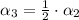
Eq. 3b in Eq. 2b:

`(p-2)\cdot \alpha_(2) = 0`

If
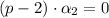
`p = 2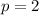` if given vectors must be linearly independent.