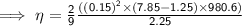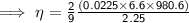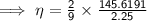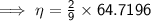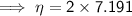Question

A ball bearing of radius of 1.5 mm made of iron of density

7.85 g cm is allowed to fall through a long column of
glycerine of density 1.25 g cm. It is found to attain a
terminal velocity of 2.25 cm s-'. The viscosity of glycerine is
​

Answer 1

`\boxed{\sf Viscosity \ of \ glycerine \ (\eta) = 14.382 \ poise}`

Given:

Radius of ball bearing (r) = 1.5 mm = 0.15 cm

Density of iron (ρ) = 7.85 g/cm³

Density of glycerine (σ) = 1.25 g/cm³

Terminal velocity (v) = 2.25 cm/s

Acceleration due to gravity (g) = 980.6 cm/s²

To Find:

Viscosity of glycerine (
`\sf \eta`)

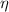Step-by-step explanation:

`\boxed{ \bold{v = (2)/(9) \frac{( {r}^(2) ( \rho - \sigma)g)}{ \eta} }}`

`\sf \implies \eta = (2)/(9) \frac{( {r}^(2)( \rho - \sigma)g )}{v}`

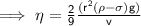
Substituting values of r, ρ, σ, v & g in the equation:

`\sf \implies \eta = (2)/(9) \frac{( {(0.15)}^(2) * (7.85 - 1.25) * 980.6)}{2.25}`

`\sf \implies \eta = (2)/(9) ((0.0225 * 6.6 * 980.6))/(2.25)`

`\sf \implies \eta = (2)/(9) * (145.6191)/(2.25)`

`\sf \implies \eta = (2)/(9) * 64.7196`

`\sf \implies \eta = 2 * 7.191`

`\sf \implies \eta = 14.382 \: poise`