Question

The area of a rectangular garden is given by the trinomial x2 + x – 42. What are the possible dimensions of the rectangle? Use factoring.

Answer 1

`\boxed{ \boxed{ \bold{ \sf{(x + 7) \: and \: (x - 6)}}}}`

Explanation:

`\sf{ {x}^(2) + x - 42}`

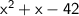
Here, we have to find two numbers which subtracts to 1 and multiplies to 42

⇒
`\sf{ {x}^(2) + (7 - 6)x - 42}`

⇒
`\sf{ {x}^(2) + 7x - 6x - 42}`

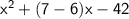
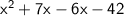
Factor out x from the expression

⇒
`\sf{x(x + 7) - 6x - 42}`

Factor out 6 from the expression

⇒
`\sf{x(x + 7) - 6(x + 7)}`

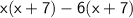
Factor out x + 7 from the expression

⇒
`\sf{(x + 7)(x - 6)}`

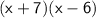
So, the possible dimensions of the rectangle are x + 7 and x - 6 .

Hope I helped!

Best regards!

Answer 2

Explanation:

Hello, please consider the following.

`x^2+x-42\\\\\text{The sum of the zeroes is -1=-7+6 and the product is -42=-7*6.}\\\\\text{So, we can factorise.}\\\\x^2+x-42\\\\=x^2+7x-6x-42\\\\=x(x+7)-6(x+7)\\\\=(x+7)(x-6)`

So, the possible dimensions of the rectangle are (x+7) and (x-6).

Thank you.