Question

The function intersects its midline at (-1.25,-3) and a maximum point at (0,4) Find a formula for f(x) Give an exact expression.

Answer 1

Answer: y = 7cos(0.4π x) - 3

Explanation:

The equation of a cosine function is: y = A cos(Bx - C) + D where

• Amplitude (A) is the distance from the midline to the max (or min)
• Period (P) is the length of one cosine wave --> P = 2π/B
• Phase Shift (C/B) is the horizontal distance shifted from the y-axis
• Midline (D) is the vertical shift. It is equal distance from the max and min

Midline (D) = -3

(-1.25, -3) is given as a point on the midline. We only need the y-value.

Horizontal stretch (B) = 0.4π

The max is located at (0,4) and also at (5, 4). Thus the period (length of one wave) is 5 units.

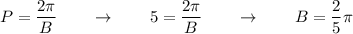`P=(2\pi)/(B)\qquad \rightarrow \qquad 5=(2\pi)/(B)\qquad \rightarrow \qquad B=(2)/(5)\pi` → B = 0.4π

Phase Shift (C) = 0

The max is on the y-axis so there is no horizontal shift.

Amplitude (A) = 7

The distance from the midline to the max is: A = 4 - (-3) = 7

Equation

Input A = 7, B = 0.4π, C = 0, and D = -3 into the cosine equation.

y = A cos(Bx - C) + D

y = 7cos(0.4π x - 0) - 3

y = 7cos(0.4π x) - 3