Question

Which of the following pairs of functions are inverses of each
other?

Answer 1

Answer: C

Explanation:

For this problem, let's find the inverse for all f(x) and see which pairs with the g(x). To find the inverse, you replace the x with y and y with x. Then you solve for y.

A. Incorrect

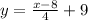`y=(x-8)/(4) +9` [replace x with y and y with x]

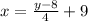`x=(y-8)/(4) +9` [subtract both sides by 9]

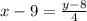`x-9=(y-8)/(4)` [multiply both sides by 4]

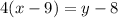`4(x-9)=y-8` [add both sides by 8]

`4(x-9)+8=y`

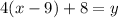
This does not match g(x), therefore, they are not inverses of each other.

----------------------------------------------------------------------------------------------------------

B. Incorrect

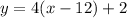`y=4(x-12)+2` [replace x with y and y with x]

`x=4(y-12)+2` [subtract both sides by 2]

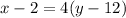`x-2=4(y-12)` [divide both sides by 4]

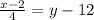`(x-2)/(4) =y-12` [add both sides by 12]

`(x-2)/(4) +12=y`

This does not match g(x), therefore, they are not inverses of each other.

----------------------------------------------------------------------------------------------------------

C. Correct

`y=3((x)/(2))-4` [replace x with y and y with x]

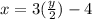`x=3((y)/(2) )-4` [add both sides by 4]

`x+4=3((y)/(2) )` [divide both sides by 3]

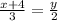`(x+4)/(3) =(y)/(2)` [multiply both sides by 2]

`(2(x+4))/(3) =y`

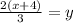
This matches g(x), therefore, they are inverses of each other.

----------------------------------------------------------------------------------------------------------

D. Incorrect

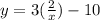`y=3((2)/(x) )-10` [replace x with y and y with x]

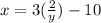`x=3((2)/(y) )-10` [add both sides by 10]

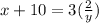`x+10=3((2)/(y) )` [divide both sides by 3]

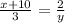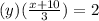`(x+10)/(3) =(2)/(y)` [multiply both sides by y]

`(y)((x+10)/(3) )=2` [multiply both sides by
`(3)/(x+10)` or divide by
`(x+10)/(3)`]

`y=(6)/(x+10)`

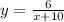
This does not match g(x), therefore, they are not inverses of each other.

----------------------------------------------------------------------------------------------------------

After going through each problem, we found that the correct answer is C.