Answer: Area =
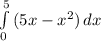
Explanation:
Thiis is quite straightforward, so I will be gudiding you through the process.
we have that;
y1 = x² -5x
and y² = 0
Taking Limits:
y1 = x² -5x, y2 = 0
x² - 5x = 0;
so x(x - 5) = 0
this gives x = 0 and x = 5
∴ 0≤x≤5
This is to say that the graph intersets at x = 0 and x = 5 and y2 is the upper most function.
Let us take the formula:
Area = ∫b-a (upper curve - lower curve)
where a here represents 0 and b represents 5
the upper curve y2 = 0
whereas the lower curve y1 = x² - 5x
Area = ∫5-0 [ 0 - (x² - 5x) ] dx
This becomes the Area.
Area =
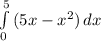
cheers i hope this helped !!!