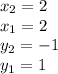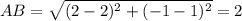Answer:
Explanation:
Given a triangle has points:
(-5,1),(2,1), (2,-1)
Let us label the points:
A(2,1),
B(-5,1) and
C(2,-1)
To find:
Distance between (−5, 1) and (2, −1) i.e. BC.
Horizontal leg AB and
Vertical leg, AC.
Solution:
Please refer to the attached diagram for the labeling of the points on xy coordinate plane.
We can simply use Distance formula here, to find the distance between two coordinates.
Distance formula :
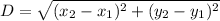
For BC:
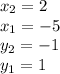
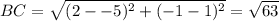
Horizontal leg, AC:
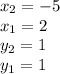
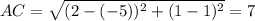
Vertical Leg, AB: