Question

When a cube is inscribed in a sphere of radius r, the length Lof a side of the cube is . If a positive point charge Qis placed at the center of the spherical surface, the ratio of the electric flux sphereat the spherical surface to the flux cubeat the surface of the cube is(sphere / cube)

Answer 1

Ф_cube /Ф_sphere = 3 /π

Step-by-step explanation:

The electrical flow is

Ф = E A

where E is the electric field and A is the surface area

Let's shut down the electric field with Gauss's law

Фi = ∫ E .dA =
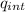`q_(int)` / ε₀

the Gaussian surface is a sphere so its area is

A = 4 π r²

the charge inside is

q_{int} = Q

we substitute

E 4π r² = Q /ε₀

E = 1 / 4πε₀ Q / r²

To calculate the flow on the two surfaces

* Sphere

Ф = E A

Ф = 1 / 4πε₀ Q / r² (4π r²)

Ф_sphere = Q /ε₀

* Cube

Let's find the side value of the cube inscribed inside the sphere.

In this case the radius of the sphere is half the diagonal of the cube

r = d / 2

We look for the diagonal with the Pythagorean theorem

d² = L² + L² = 2 L²

d = √2 L

we substitute

r = √2 / 2 L

r = L / √2

L = √2 r

now we can calculate the area of ​​the cube that has 6 faces

A = 6 L²

A = 6 (√2 r)²

A = 12 r²

the flow is

Ф = E A

Ф = 1 / 4πε₀ Q/r² (12r²)

Ф_cubo = 3 /πε₀ Q

the relationship of these two flows is

Ф_cube /Ф_sphere = 3 /π