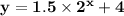Question

HELP! Determine the equation of the exponential function with a common ratio of 2, a horizontal asymptote at y = 4, and passing through the point (2, 10).

Answer 1

`\bold{y=1.5* 2^x+4}`

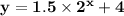
Explanation:

Equation for an exponential function is given as following:

`y=ab^x+c`

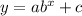
Where b is the common ratio and

c is the horizontal asymptote (y value)

a is the coefficient of exponential term of
`x`

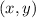`(x,y)` are the points on the function.

Here, we are given that:

Common ratio, b = 2

Horizontal asymptote at y, c = 4

So, the equation becomes (let us put the values of b and c):

`y=a* 2^x+4`

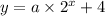
We need the value of a. Let us put value of (x,y) as (2,10).

`10=a* 2^2+4\\\Rightarrow a* 4 =10-4 =6\\\Rightarrow a =(6)/(4) =\bold{1.5}`

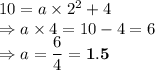
So, the final equation of the exponential function is:

`\bold{y=1.5* 2^x+4}`