Question

A tree is broken at a height of 5 meters from the ground and it's top touches the ground existence of 12 m from the base of the tree find the original height of the tree

Answer 1

18 m

Explanation:

The given situation is equivalent to a right angled triangle as shown in the diagram attached.

AB is the height at which tree was cut.

And the top touches the ground at a point C.

So,

AB = 5 m and

AC = 12 m

Here, we have to find original height of the tree.

Original height of Tree = AB + BC OR AB + BC' (Because B is the point in height AC' of tree)

Let us consider the
`\triangle ABC`.

As per pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)\\\Rightarrow BC^(2) = AB^(2) + AC^(2)\\\Rightarrow BC ^2=5^2+12^2\\\Rightarrow BC = √(169)\\\Rightarrow BC = 13\ m`

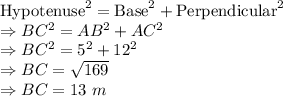
Therefore the answer is :

Height of tree = 5+13 = 18 m