Question

Two different red-light-running signal systems were installed at various intersection locations with the goal of reducing angle-type crashes. Red-Light-Running System A resulted in 60% angle crashes over a sample of 720 total crashes. Red-Light-Running System B resulted in 52% angle crashes over a sample of 680 total crashes. Was there a difference between the proportions of angle crashes between

Answer 1

Complete Question

Two different red-light-running signal systems were installed at various intersection locations with the goal of reducing angle-type crashes. Red-Light-Running System A resulted in 60% angle crashes over a sample of 720 total crashes. Red-Light-Running System B resulted in 52% angle crashes over a sample of 680 total crashes. Was there a difference between the proportions of angle crashes between the two red-light-running systems installed? Use an alpha of 0.10.

Answer:

Yes there is a difference between the proportions of angle crashes between the two red-light-running systems installed

Explanation:

From the question we are told that

The first sample proportion is
`\r p_ 1 = 0.60`

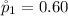
The second sample proportion is
`p_2 = 0.52`

The first sample size is
`n_1 = 720`

The second sample size is
`n_2 = 680`

The level of significance is
`\alpha = 0.10`

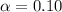
The null hypothesis is
`H_o : \r p_1 - \r p_2 = 0`

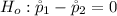
The alternative hypothesis is
`H_a : \r p_1 - \r p_2 \\e 0`

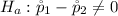
Generally the pooled proportion is mathematically represented as

`p_p = ((\r p_1 * n_1 ) + (\r p_2 * n_2))/(n_1 + n_2 )`

=>
`p_p = ((0.6 * 720) + ( 0.52 * 680))/(720 +680 )`

=>
`p_p = 0.56`

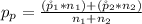
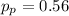
Generally the test statistics is evaluated as

`t = \frac{ ( \r p_1 - \r p_2 ) - 0 }{ \sqrt{ (p_p (1- p_p) * [ (1)/(n_1 ) + (1)/(n_2 ) ])} }`

`t = \frac{ (0.60 - 0.52 ) - 0 }{ \sqrt{ (0.56 (1- 0.56) * [ (1)/(720) + (1)/(680 ) ])} }`

`t = 3.0`

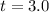
The p-value obtained from the z-table is

`p-value = P(Z> t ) = 0.0013499`

From the question we see that
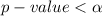`p-value < \alpha` so the null hypothesis is rejected

Hence we can conclude that there is a difference between the proportions