Question

There are three motors available to repair Ralph’s vacuum cleaner. Motor #1 has a 65% chance of breaking by the end of the week. Motor #2 has a 35% chance of breaking by the end of the week. Motor #3 has a 5% chance of breaking by the end of week. Suppose that Ralph randomly chooses one of the three motors so that each is equally likely, and then the motor does break by the end of the week. What is the conditional probability that Ralph installed motor #1?

Answer 1

0.619

Explanation:

from the question we have the following data:

probability of motor 1 breaking = 65% = 0.65

probability of motor 2 breaking = 35% = 0.35

probability of motor 3 breaking = 5% = 0.05

since we have 3 motors the probability of any of them breaking down is =
`(1)/(3)`

but what the question requires from us is the conditional probability of the first one being installed

we have to solve this questions using bayes theorem

such that:

`(0.65*(1)/(3) )/(0.65*(1)/(3)+0.35*(1)/(3)+0.05*(1)/(3) )`

=
`(0.2167)/(0.2167+0.1167+0.0167)`

=
`(0.2167)/(0.3501)`

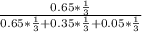
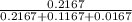
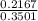
= 0.618966

approximately 0.619

therefore the conditional probability ralph installed the first motor is 0.619