Question

Find the positive numbers such that the sum of and its reciprocal is as small as possible.Does this problem require optimization over an open interval or a closed interval

Answer 1

Yes and closed interval

Explanation:

The computation is shown below:

For the sum and the reciprocal as small as the possible equation is as follows

`\((d)/(dx)\left(x+(1)/(x)\right)=0.\)`

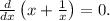
Now take out the derivates,

So,

`\(1-(1)/(x^2)=0,\)`

or we can say that

`\(x^2-1=0\rightarrow x=\pm1.\)`

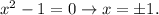
As the only positive number is to be determined i.e

x = 1

So this problem needed the optimization over a closed interval and the same is to be considered.