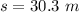Question

The floor of a railroad flatcar is loaded with loose crates having a coefficient of static friction of 0.420 with the floor. If the train is initially moving at a speed of 57.0 km/h, in how short a distance can the train be stopped at constant acceleration without causing the crates to slide over the floor

Answer 1

The distance is
`s= 30.3 \ m`

Step-by-step explanation:

From the question we are told that

The coefficient of static friction is
`\mu_s = 0.42`

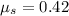
The initial speed of the train is
`u = 57 \ km /hr = 15.8 \ m/s`

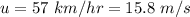
For the crate not to slide the friction force must be equal to the force acting on the train i.e

`-F_f = F`

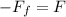
The negative sign shows that the two forces are acting in opposite direction

=>
`mg * \mu_s = ma`

=>
`-g * \mu_s = a`

=>
`a = -9.8 * 0.420`

=>
`a = -4.116 m/s^2`

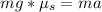
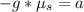
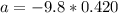
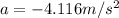
From equation of motion

`v^2 = u^2 + 2as`

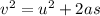
Here v = 0 m/s since it came to a stop

=>
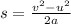
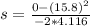
`s= (v^2 - u^2 )/( 2 a)`

=>
`s= (0 -(15.8)^2 )/( - 2 * 4.116)`

=>
`s= 30.3 \ m`