Hey ! there
Answer:
- Area of rectangle is 1008 m²
Explanation:
In this question we are given that length of rectangle is reduced by its breadth by 8 m and Perimeter of rectangle is 128 m.
And we are asked to find the area of the rectangle.
For finding the area of rectangle firstly we need to find the length and breadth of the rectangle but their value aren't given . So we are assuming,
- Length as ( x - 8 ) metres ( Because in question it is given that length of rectangle is reduced by its breadth by 8 m )
Solution : -
Finding Length and Breadth : -
We know that ,

Where ,
According to question , perimeter of rectangle is 128 m. So ,
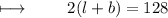
Substituting value of length and breadth :

Solving parenthesis :
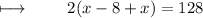
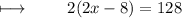
Dividing with 2 on both sides :

We get ,
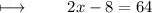
Adding 8 on both sides :
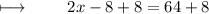
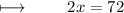
Dividing with 2 on both sides :
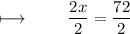
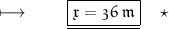
We know that ,
- So , Breadth is 36 metres .
- So , Length of rectangle is 28 metres .
Finding Area : -
We know that ,
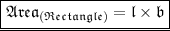
Where ,
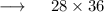
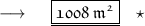
- Henceforth , area of rectangle is 1008 square metres .
#Keep Learning