Answer:
The present population of the country is 26,000.
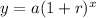
The growth rate is approximately 12%.
The population 5 years from today will be 45,821.
Explanation:
(1)
The present population of the country is 26,000.
(2)
It is provided that the number of people living in a country is increasing each year exponentially.
Then the exponential growth function can be used to describe the situation.
The exponential growth function is:
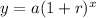
Here,
y = final value
a = initial value
r = growth rate
x = time
(3)
It is provided that x = 5 years ago the population was a = 15,000 and at present the population is y = 26,000.
Compute the value of r as follows:
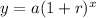
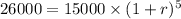
![(1+r)=[(26000)/(15000)]^(1/5)](https://img.qammunity.org/2021/formulas/mathematics/high-school/bt6exsxg4kc0t87yf79722d7sje9m2d53x.png)
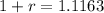

Thus, the growth rate is approximately 12%.
(4)
Compute the population 5 years from today as follows:
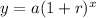

Thus, the population 5 years from today will be 45,821.