Answer:
A) x intercept: (2, 0) , (-2, 0)
y intercept: (0, 16)
B) symmetric about y axis
Explanation:
Given the function:
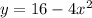
To find:
Algebraically, A) find the x and y intercepts and B) the symmetry type.
Solution:
A) x intercept, let us put y = 0
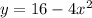
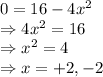
x intercept: (2, 0) , (-2, 0)
For y intercept, put x = 0
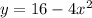
y = 16 - 0 =16
y intercept: (0, 16)
B) If the quadratic equation is given as:
 ,
,
the axis of symmetry is a vertical line

Here, c = 16
b = 0 and
a = -4
So, Axis of symmetry is:
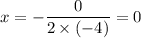
which is the equation of y axis.
So, given equation is symmetric about y axis.