Complete Question
It has been found from experience that the mean breaking strength of a particular brand of thread is 9.72 oz with a standard deviation of 1.4 oz. Recently a sample of 36 pieces of thread showed a mean breaking strength of 8.93 oz. Can one conclude at a significance level of (a) 0.05, (b) 0.01 that the thread has become inferior?
Answer:
At both
 and
and
 the conclusion is that the thread has become inferior
the conclusion is that the thread has become inferior
Explanation:
From the question we are told that
The population mean is
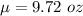
The standard deviation is

The sample size is n = 36
The sample mean is
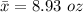
The null hypothesis is
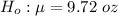
The alternative hypothesis is

Generally the test statistics is mathematically represented as

=>
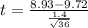
=>

So
The p-value obtained from the z- table is

So at
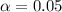
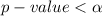
So we reject the null hypothesis,hence we conclude that the thread has become inferior
So at
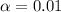
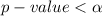
So we reject the null hypothesis,hence we conclude that the thread has become inferior